Testing and Targets
Test Target Overview
This is Section 12.2 of the Imaging Resource Guide.
Test targets help determine the performance of an imaging system. This includes troubleshooting a system; benchmarking, certifying, or evaluating measurements; or establishing a foundation to ensure multiple systems work well with one another. Because image quality can be defined by different components, particularly resolution, contrast, modulation transfer function (MTF), depth of field (DOF), or distortion, different systems may require different targets. Some systems may require more than one. Note that the results of using a test target are subjective if only viewed visually; using visual observation is dependent on who is looking at the target. Someone with 20/20 vision is typically capable of discerning higher resolution or more detail than someone with 20/25 or 20/30 vision. Additionally, individuals that regularly look at these targets may have trained their brains to interpolate details not actually present due to viewing the target’s repetitive patterns. Visual inspection can help compare two different systems but does not always validate results. It is important to use software to truly validate measurements.
| Targets for Resolution Measurements | |||
| Target | Applications | Pros | Cons |
| USAF 1951 | Test resolution in vision systems, optical test equipment, microscopes, high magnification video lenses, fluorescence and confocal microscopy, photolithography, and nanotechnology | Simultaneously test the vertical and horizontal resolutions at discrete spatial frequencies | Must reposition target to fully evaluate a system’s performance |
| Can be difficult to determine when the entire FOV is in best focus | |||
| Ronchi Ruling | Testing resolution and contrast | Can simultaneously determine system’s best focus across entire FOV | Different target required for each frequency that needs to be evaluated |
| Diffraction testing | Non-symmetrical resolution reductions cannot be analyzed | ||
| Star | Comparing highly resolved or magnified imaging systems | Potentially most powerful for testing resolution and contrast | Difficult to determine exact resolution that the test system is achieving at each element |
| System alignment | Can evaluate continuous change in resolution across multiple orientations without repositioning target | ||
| Assembly assistance | Eases the comparison of different imaging systems | Requires advanced image analysis software | |
Table 1: Applications and the pros and cons of different resolution targets.
The USAF 1951 Target
This is Section 12.3 of the Imaging Resource Guide.
The USAF 1951 target is one of the most common test targets used and is comprised of sets of horizontal and vertical lines, called elements, of varying sizes (Figure 1).

Figure 1: Example of a USAF 1951 target.
The horizontal and vertical elements are used by a system to simultaneously test the vertical and horizontal resolutions at discrete spatial frequencies (line pairs per millimeter, or $ \small{ \tfrac{\text{lp}}{\text{mm}} } )$ in the object plane. Each element has a unique set of widths and spacings and is identified with a number from 1 to 6. Six sequentially numbered elements are considered a group and each group has an identifying number that can be positive, negative, or zero. This group number ranges from -2 to 7. The group number and element number are then used together to determine spatial frequency. The resolution is based on one line pair (lp) which is equivalent to one black bar and one white space (Figure 2).
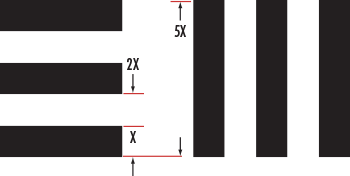
Figure 2: USAF 1951 target specifications.
Vertical bars are used to calculate horizontal resolution, and horizontal bars are used to calculate vertical resolution.
Qualitatively, the resolution of an imaging system is defined as the group and element combination that is located directly before the black and white bars begin to blur together. Quantitatively, resolution (in $ \small{ \tfrac{\text{lp}}{\text{mm}} } )$ can be calculated with Equation 1, where $\small{\xi} $, is resolution in $ \small{ \tfrac{\text{lp}}{\text{mm}} }$, $\small{G}$ is the group number and $ \small{E} $ is the element number.
USAF 1951 targets are designed so that higher-resolution elements are closer to the center of the target while lower-resolution elements are closer to the target edges. This arrangement is beneficial for testing zoom lenses because it avoids the need to reposition the target by allowing the higher resolution elements to remain in the FOV as the lens magnification decreases the FOV.
Limitations of USAF 1951 Targets
USAF 1951 targets do have drawbacks from the higher-resolution elements being centered. Lenses produce different levels of resolution at the center and corners of the FOV. Moving away from the center of the field usually causes resolution to decrease, making it important to check resolution and contrast at many field positions. This requires repositioning the target around the FOV and taking multiple images to evaluate a system’s full performance, increasing testing time. This can also cause issues depending on whether the system is focused at the center of the FOV or across the entire field; because resolution varies across the field, it can be difficult to determine when the full FOV is in best focus. Some lenses obtain very high resolution at the center of the FOV, but very low resolution at the corners when the lens and camera system is focused on the center of the image. Defocus the lens slightly to balance the resolution across the full field. However, doing this is at the detriment of the center resolution. The loss of center resolution is not necessarily bad though, because the lens may still meet the demands of the application while still achieving a balanced focus (Figure 3).

Figure 3a: USAF 1951 Example: The center and corner of an image that has been repositioned so that the best focus is only in the middle of the target.

Figure 3b: The center and corner of an image that features balanced focus across the entire field.
The potential for resolution variability across the FOV reinforces the need to analyze all field positions before drawing conclusions on a system’s performance. The lens that performs optimally with the target at the center may not perform the best overall. However, it is critical to perform all the analysis at a single focus setting. It may seem intuitive to determine the system’s best performance through the middle of the lens and then refocus to see the performance in the corner, but this will not show how the system will perform once deployed because refocusing during operation is often not possible.
There are variations of this target that allow for analysis across the entire FOV by repeating the patterns in numerous locations on the target (Figure 4).

Figure 4a: A USAF 1951 pattern wheel target.
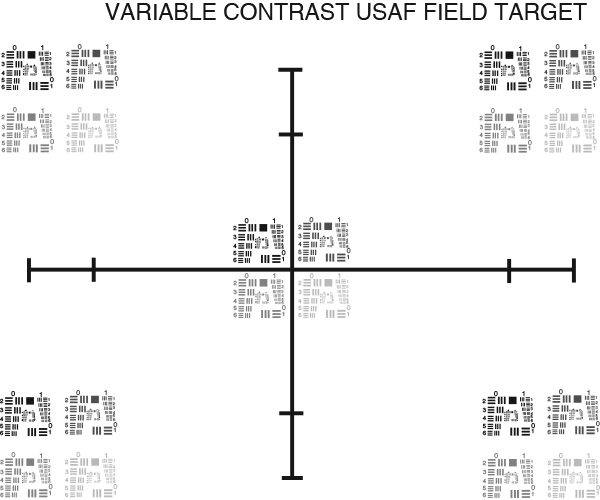
Figure 4b: A USAF 1951 variable contrast and field target.
Ronchi Rulings
This is Section 12.4 of the Imaging Resource Guide.
Some issues associated with the USAF 1951 target are overcome using the target known as a Ronchi ruling. This target has repeating lines at one spatial frequency in one orientation that covers the target’s full surface (Figure 5). Because there is detail across the full target, the system’s best focus across the full field can be evaluated. For applications needing only one frequency analyzed, this is an easy-to-use, straightforward tool. However, there are two drawbacks to using the Ronchi ruling. First, since a given target provides only one frequency, a new target is required for each frequency. Second, non-symmetrical resolution reductions across the field that are the result of factors such as astigmatism cannot be analyzed because the lines only propagate in one direction. To overcome this, the target must be rotated by 90° and a second image must be used to analyze the resolution. Additionally, while a lens’ focus can be balanced for best focus, even for cases of astigmatism, it can be difficult to find this balance when alternating back and forth.

Figure 5: A Ronchi ruling.
The Star Target
This is Section 12.5 of the Imaging Resource Guide.
The multi-element start target is possibly the most powerful tool for testing the resolution and contrast of a system and combines many of the strengths of both the USAF and Ronchi targets. Each element of the star target consists of a circle formed of alternating positive and negative pie-shaped wedges that are tapered towards the center at a known angle (Figure 6). The element’s tapered wedges provide a continuous change in resolution that can be evaluated in both vertical and horizontal directions, along with a variety of other orientations, without repositioning the target.
Having many stars across the FOV makes comparing different imaging solutions easier by providing the ability to determine the best focus across the FOV while simultaneously analyzing horizontal and vertical information at a variety of resolutions. Figure 4 shows the complete star target; the highlighted areas located in the center, bottom middle, and the corner of the target are compared between two different lenses in the additional example images. For these examples, a Sony ICX625 monochrome sensor with 3.45µm pixels and a total resolution of 5MP and a white light back light illuminator are used.

Figure 6: A star target.
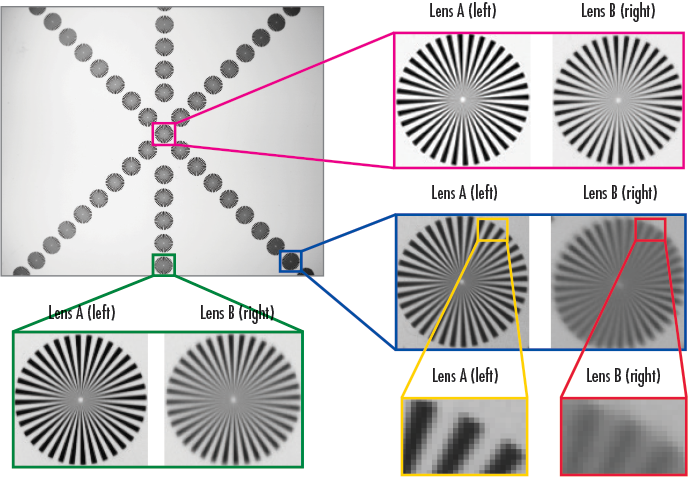
Figure 7: A star target is imaged with two lenses (A and B) with the same focal length, f/#, FOV, and sensor. The superiority of lens A becomes apparent along the edge and in the corner of the sensor.
Limitations of the Star Target
The star target also has its drawbacks. Because the wedges provide continuous changes in resolution, it is more difficult to determine the exact resolution that the test system is achieving at each element. While this can be done mathematically, it is not visually done with ease. Additionally, the combination of the star elements’ circular nature with the potential for nonsymmetrical blurring make using simple software tools, such as line profilers, to extract information from the image more difficult. More advanced image analysis software is required to make full use of the star target.
Telecentricity Targets
This is Section 12.6 of the Imaging Resource Guide.
Telecentricity targets allow keystoning in an image to be visualized and accurately measured. The amount of keystoning is related to the telecentricity of the lens imaging the target. The target is placed at a 45° angle to the optical axis so that the bottom of the target is further away from the lens than the top of the target (Figure 8).

Figure 8: A telecentricity target placed under a lens.
When imaging the target through a non-telecentric lens, the distance between the vertical lines will appear to decrease at the bottom of the image (Figure 9); this effect is known as keystoning. A perfectly telecentric lens will have no keystoning and the telecentricity will be 0° (Figure 10).

Figure 9: This image (taken with an 8mm focal length lens) demonstrates keystoning. The lines clearly converge at the bottom of the image. The center location of a line at the bottom of the image does not have the same center location at the top of the image.

Figure 10: It is apparent that the blur in this image (taken with a telecentric lens) is symmetric. If you take a horizontal line profile across the image and find the horizontal component of the center of each black line, the location will be equal in the blurred part of the image and the focused part of the image.
This difference in position can be converted to a degree of telecentricity with the following steps:
- Find the distance between your top line profile and your bottom line profile. $ \Delta Y = \left( Y_1 - Y_2 \right) $
- Find the horizontal displacement. $ \Delta X = \left| X_1 - X_2 \right| $
- Calculate the telecentric angle. $ \theta = \tan ^{-1} \left( \tfrac{\Delta X}{\Delta Y} \right) $
Depth of Field Targets
This is Section 12.7 of the Imaging Resource Guide.
DOF targets enable the visualization and quantification of how well focus is maintained as details move away from the plane the lens is focused on. DOF targets consist of lines of known frequencies resolutions) that are tipped at a known angle and are used to determine how well focus is maintained. As the lines proceed closer to and farther away from the lens, the blurrier they become, until they are no longer able to be distinguished from one another. Contrast measurement can be made at different distances to determine when the desired level of resolution is lost; this determines the DOF limit for a lens at a setting. Figures 11 and 12 demonstrate how to use a DOF target.

Figure 11: A DOF target should be at 45° from the lens.
Figure 12: Sample configurations using a DOF target.
Example: Using a DOF Target
50mm DG Series Lens
Figure 13 shows a vertically mounted camera looking down at a DOF target that has been set at a 45° angle to the imaging path. Since the lens is focused at the middle of the target vertically, the image goes out of focus at the top and bottom of the target. The images show three different f/# settings and how adjustments to the iris change the ability to obtain DOF. Note: Ronchi rulings can also be used to perform this type of testing, as they have fixed frequencies and can be tilted to create this effect; the greater the tip, the more of the DOF that can be measured.
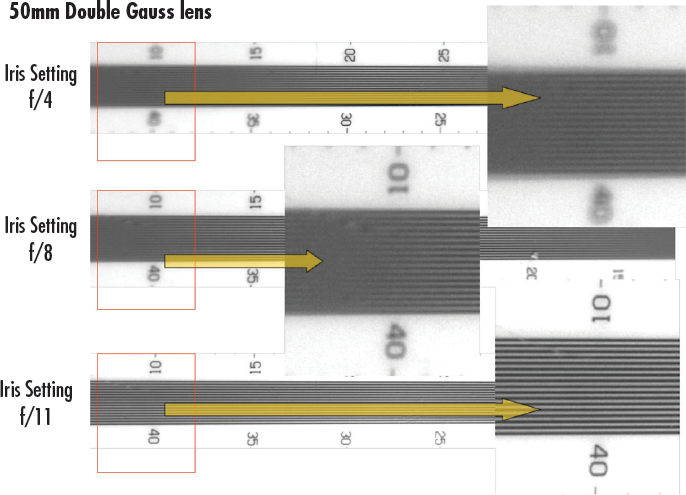
Figure 13: Images of a DOF target taken with a 50mm lens at f/4, f/8, and f/11.
Go to www.edmundoptics.com/imaging-lab to view Edmund Optics Imaging Lab Module 1.8 on Depth of Field.
Distortion Targets
This is Section 12.8 of the Imaging Resource Guide.
Distortion targets are used to calibrate systems to correctly measure the optical misplacement of imaging information. These targets consist of dot, grid, or square patterns; are compatible with the calibration routines of most imaging software; and can either remap or adjust measurements across the FOV (Figure 14).

Figure 14: A dot grid distortion target.
Figure 15 shows the types of distortion that can be adjusted. Once the pattern is imaged, the known size and spacing of the pattern allow adjustments to be made (Figure 15).
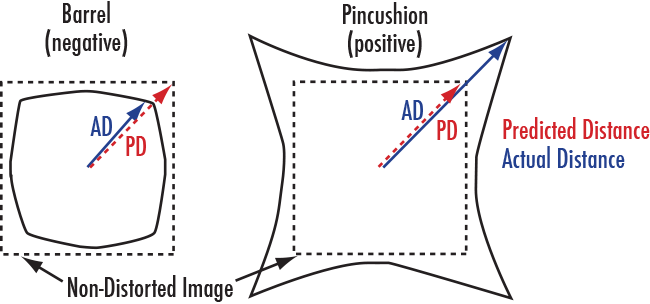
Figure 15: Types of distortion.














 Previous Section
Previous Section 


















or view regional numbers
QUOTE TOOL
enter stock numbers to begin
Copyright 2023 | Edmund Optics, Ltd Unit 1, Opus Avenue, Nether Poppleton, York, YO26 6BL, UK
California Consumer Privacy Acts (CCPA): Do Not Sell or Share My Personal Information
California Transparency in Supply Chains Act